Poker Hands Odds
As a poker player, knowing poker hand odds and rankings is crucial to knowing where you stand when calculating your odds of winning. This guide is for players from beginner to intermediate level – meaning those with a basic knowledge of poker but who don’t know how best to calculate poker odds to gauge the chances of success – and will give you everything you need to beat others when playing online poker.
How Odds Work
Poker odds give you the probability of winning any given hand. Higher odds mean a lower chance of winning, meaning that when the odds are large against you it’ll be a long time until you succeed. They are usually displayed as a number to number ratio and indicate the potential return on investment; for example, odds of nine to one (9:1) means that for every $1 wagered you’ll be paid $9.
Before you can begin to understand poker odds, you’ll need to learn how to calculate ‘outs’. Outs are the cards that can help you improve your hand and make it more valuable than what you believe your opponent has. There are 52 cards in a deck and two of those will be in your hand when starting playing, with a further four cards exposed from the flop and turn. That means that of the 37 cards that remain unseen, there are 9 potential winning cards or ‘outs’. That equates to odds of 4:1 for getting one of the cards, or outs, you need.
Poker Odds Chart
If you need to know some of the odds and probabilities of common poker hands, take a look at our poker odds chart to quickly learn which hands to play. You can either print it out and keep it to hand during a game, or calculate poker odds at a glance online.
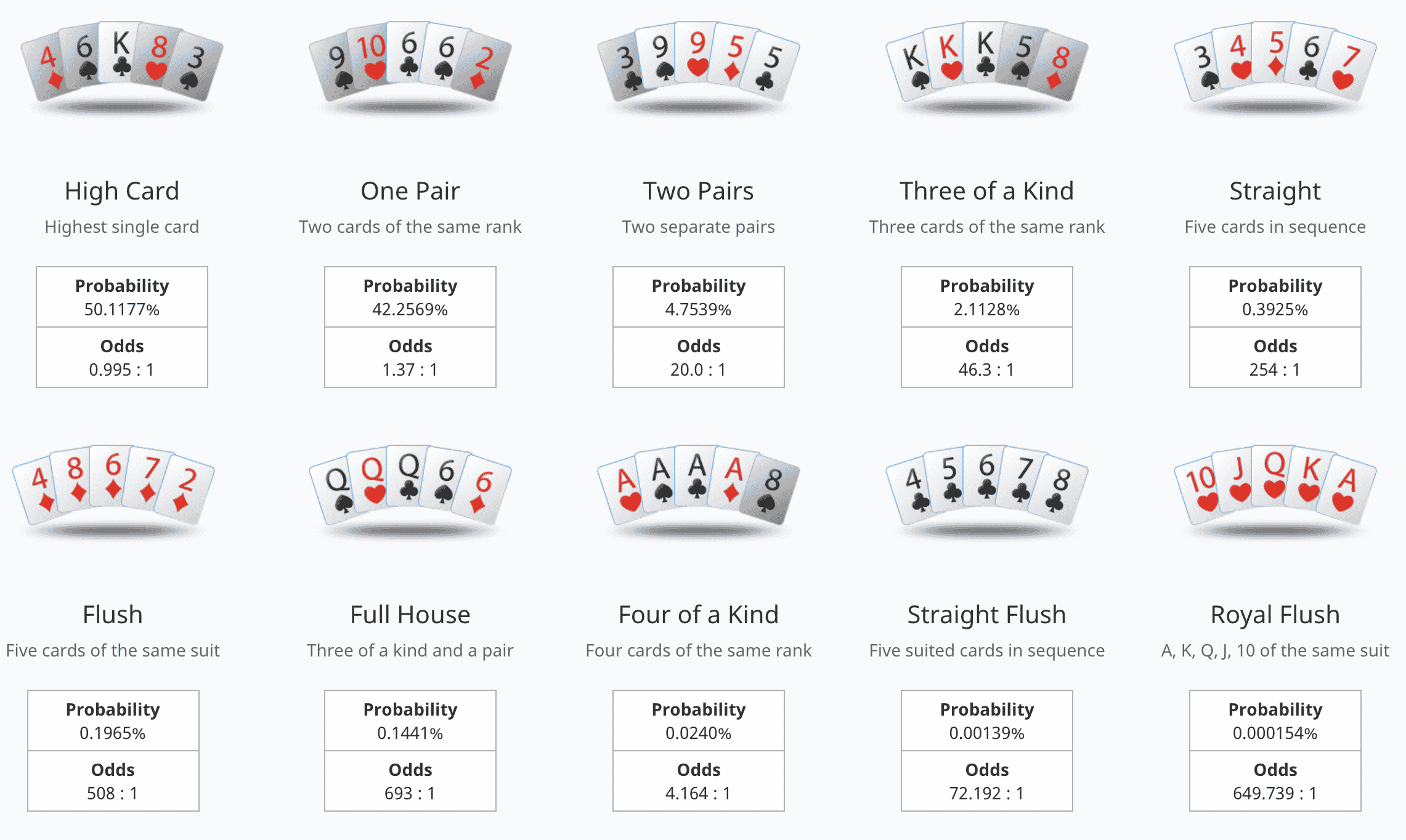
Common Poker Hands Odds
To help you become a better player, we’ve listed the odds of common poker hands and situations that you’re likely to see at the table. To learn more about key tactics and terms when playing poker, visit our poker school.
Open-ended straight draws (4.8:1)
An open-ended straight draw (OESD) is a straight draw that can be completed at either end. For example, holding 6, 7, 8 and 9 means either a 10 or 5 will complete the straight. There are eight outs: the four fives and the four tens. However, you should be aware that these odds presume that there is no possible flush on the board and that you’re drawing to the best hand, which may not be the case.
Four to a flush (4.1:1)
A four-flush (flush draw) is a hand that is one card short of being a full flush. If your hole cards (which you are dealt at the beginning of a hand) are suited and there are two more of your suit on the board, this is a good hand, as it’s rare that another player will have two hole cards of your suit. However, you should be cautious if you don’t have the ace as this will lower your odds of winning.
Inside straight (10.5:1)
Also known as a gutshot, an inside straight is four cards that form a straight with one of the middle three cards missing. For example, 8, 9, 10, J and Q is a straight – removing the 8 or Q makes it an outside straight, and removing the 9, 10 or J makes it an inside straight. Again, these odds assume that you’re aiming to draw the best hand possible, but unless you use both of your hole cards to make the straight, that won’t be the case.
One pair to two pair or trips (8.2:1)
A two pair is the seventh-best possible poker hand and is formed with two cards of the same value. For example, if you have J-T and you suspect an opponent holds a pair of aces, you have five outs to beat him: three tens and two jacks. However, this is based on your opponent not having AJ or AT, which can be a dangerous assumption.
Overcards (6.7:1)
‘Overcard’ refers to hole cards which are of higher rank than any other cards on the board. For example, if you’re holding Ace and Queen and the flop comes 10, 8 and 6, there are two overcards on the board. Depending on what you believe your opponent has, you have six outs and odds of 6.7:1 – but this only holds true if your assumption is correct.
Drawing to a set (22:1)
A player is drawing if they have an incomplete hand and require further cards to complete it. It is often a really far-fetched draw and rarely warrants playing. Generally, if you can’t make an accurate deduction of your opponent’s hands when drawing to a set, you should always assume they have one that threatens your own and fold to avoid losing.
Hole Cards Probability
Learn more about the probability of being dealt specific hole cards.
| Hand | Probability | Odds |
|---|---|---|
| AKs (or any specific suited cards) | 0.00302 | 330.5 : 1 |
| AA (or any specific pair) | 0.00452 | 220 : 1 |
| AKs, KQs, QJs, or JTs (suited cards) | 0.0121 | 81.9 : 1 |
| AK (or any specific non-pair incl. suited) | 0.0121 | 81.9 : 1 |
| AA, KK, or QQ | 0.0136 | 72.7 : 1 |
| AA, KK, QQ or JJ | 0.0181 | 54.25 : 1 |
| Suited cards, jack or better | 0.0181 | 54.25 : 1 |
| AA, KK, QQ, JJ, or TT | 0.0226 | 43.2 : 1 |
| Suited cards, 10 or better | 0.0302 | 32.2 : 1 |
| Suited connectors | 0.0392 | 24.5 : 1 |
| Connected cards, 10 or better | 0.0483 | 19.7 : 1 |
| Any 2 cards with rank at least queen | 0.0498 | 19.7 : 1 |
| Any 2 cards with rank at least jack | 0.0905 | 10.1 : 1 |
| Any 2 cards with rank at least 10 | 0.143 | 5.98 : 1 |
| Connected cards (cards of consecutive rank) | 0.157 | 5.98 : 1 |
| Any 2 cards with rank at least 9 | 0.208 | 3.81 : 1 |
| Not connected nor suited, at least one 2-9 | 0.534 | 0.873 : 1 |
